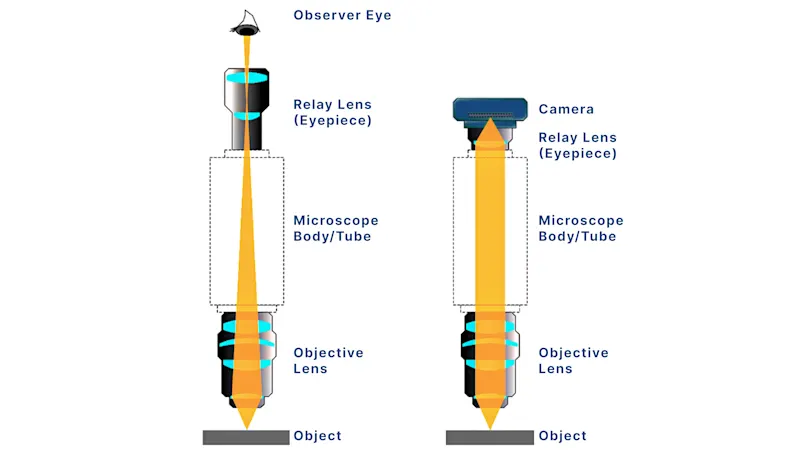
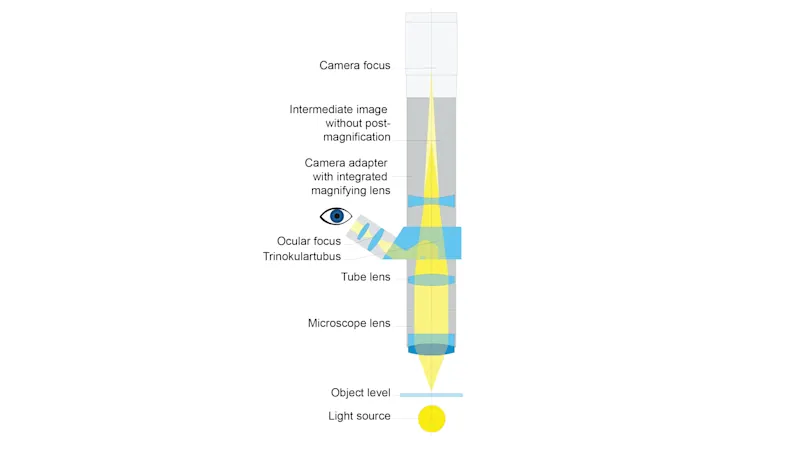
Magnification, Numerical Aperture (NA) and Resolution in Microscopic Imaging
In microscopic imaging, engineers often confuse magnification with resolution, mistakenly assuming that increasing magnification automatically reveals finer details. This misconception leads to inefficient system setups and missed features in critical applications like semiconductor inspection, biomedical imaging, and precision metrology. This article clarifies the relationships between magnification, numerical aperture (NA), and resolution, and guide vision engineers in designing high-performance vision systems at micron and sub-micron scales.
显微成像中的放大倍率
显微成像的核心在于通过放大倍率获得样品的放大图像。放大分为光学放大与数字放大两种。数字放大依赖插值算法,无法增加图像真实细节,不适用于精密检测场景,因此本文将聚焦于光学放大。
光学放大倍率
光学放大指图像在抵达传感器之前经物理方式放大,该过程通过物镜与管镜共同实现。根据系统配置是采用标准厂商物镜还是自定义镜头组,可选择以下两种方法计算系统放大倍率:
A. 使用制造商规格(标准系统)
多数工业与研究用显微镜采用无限远校正光学系统,物镜会标称其放大倍率(如10×、20×、50×)。该标称值基于标准管镜焦距(通常为200 mm,部分厂商采用180 mm或165 mm)。
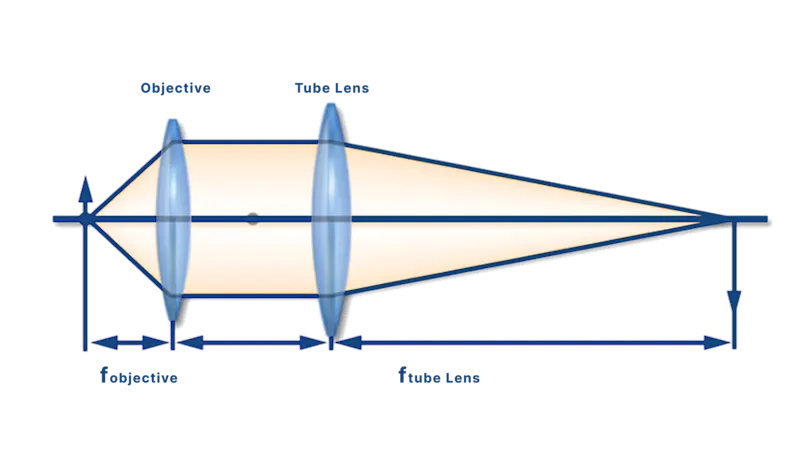
B. Using focal lengths directly (custom or OEM optics)
In many OEM or custom vision systems (e.g., machine vision), engineers often bypass manufacturer magnification values and calculate magnification using fundamental lens optics:
Msystem=ftube lens / fobjective
Where:
ftube lens: Focal length of the tube lens or relay lens
fobjective: Focal length of the objective lens
This method provides flexibility when integrating custom optics or designing compact systems without standardized components.
Example:
A 200 mm tube lens with a 20 mm objective gives: M = 200 / 20 = 10×
A 100 mm tube lens instead yields: M = 100 / 20 = 5×.
Tube lenses or adapters are often labeled 0.5×, 1×, 2×, etc., which corresponds to how they scale the final image based on the above ratio.
When building a vision system, use manufacturer-based formulas for standard setups and focal length ratios for custom designs—especially in OEM and machine vision contexts. Both methods are accurate when used consistently. The key is selecting the model that aligns best with your system’s integration and performance goals.

重要设计考量
更高有效放大倍率会缩小视场(FoV),大范围检测时可能需多次图像拼接;
仅提高放大倍率而不增加数值孔径(NA)无法提升分辨率,仅将相同分辨率信息分摊至更多像素(过采样);
系统设计需满足尼奎斯特采样准则:最小可分辨特征至少对应2像素,以避免混叠。
具体应用需求不同:
若仅为检测颗粒(如存在/缺失),1 µm/像素的分辨率或已足够;
若需检测形状、边缘或细微图案,则必须满足尼奎斯特采样以准确解析细节并避免信息丢失。
示例:
需成像1 µm特征,使用像元尺寸3.45 µm的500万像素相机时,至少需:
3.45 µm / 1 µm = 3.45 ⇒ 至少需6.9×放大倍率
这可确保1 µm特征在传感器上覆盖至少6.9 µm,满足2像素规则。
分辨率与数值孔径(NA)
在机器视觉中,放大倍率控制特征在传感器上的显像大小,而数值孔径(NA) 才真正决定系统分辨细微结构的能力。本节将探讨NA如何影响分辨率,以及如何针对不同成像场景优化其配置。
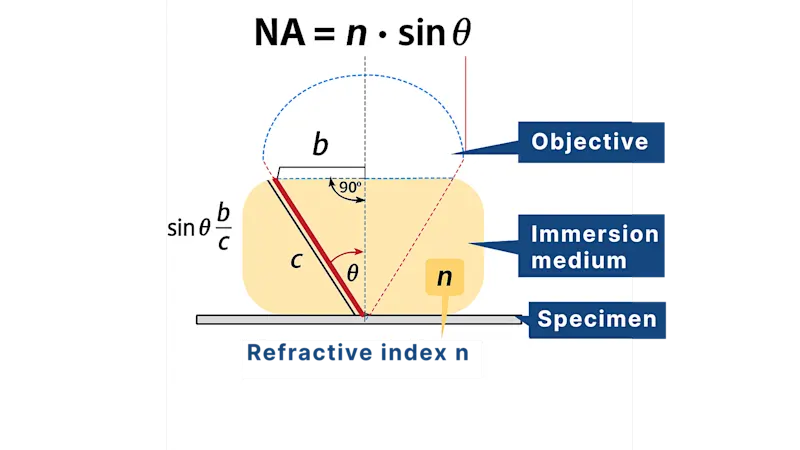
What is NA?
Numerical Aperture (NA) measures the lens’s ability to gather light and resolve fine detail. It directly impacts resolution, image sharpness, and brightness. The greater the value of NA, the greater the resolution of the result image. NA can be calculated as:
NA = n ∙ sin 𝜽
Where:
n: Refractive index of the medium between the objective lens and the sample. (air = 1.0, oil = ~1.5)
𝜽: Half-angle of light cone collected by the lens
NA increases when:
Using a medium with a higher refractive index (n) than air (e.g., immersion oil or water).
Increasing the aperture diameter.
Reducing working distance, allowing steeper light angles into the lens.
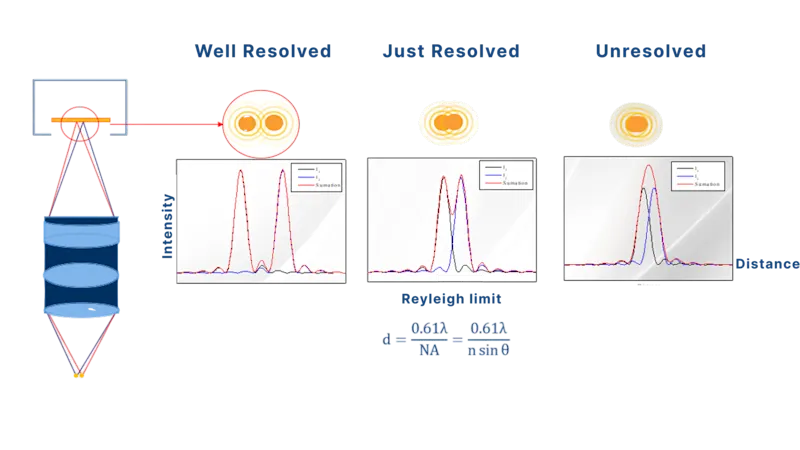
Resolution as a function of NA
Optical resolution is limited by diffraction:
Resolution=0.61⋅λ/ NA = 0.61⋅λ/ (n ∙ sin 𝜽)
Where:
λ: the illumination wavelength
A higher NA enables the resolution of smaller features— a critical factor in applications such as wafer inspection or metrology, where edge sharpness and fine pattern distinction are required.
However, optical resolution improvements only translate to usable image detail when the sensor’s pixel size and magnification meet the system’s resolving power (Nyquist sampling must be satisfied).
Note: This resolution formula originates from diffraction theory and the Rayleigh criterion, which models how light forms patterns like the Airy disk. These concepts will be covered in an upcoming advanced article on optical diffraction and imaging limits.
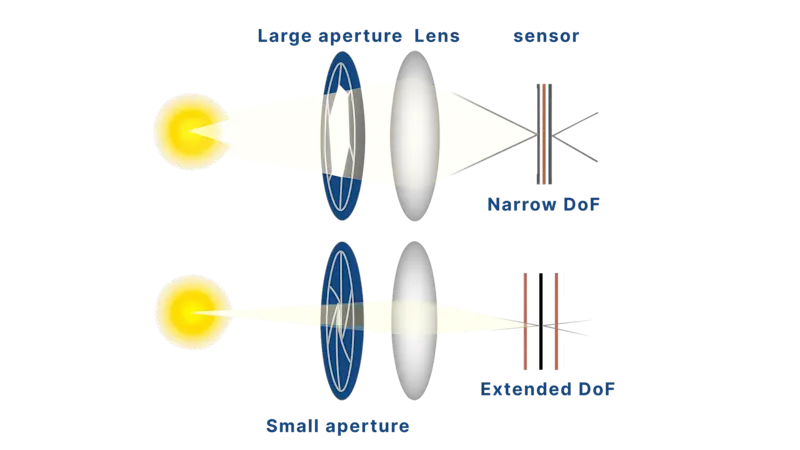
Does increasing NA solve everything?
Not entirely. While NA improves resolution and brightness, it comes with trade-offs:
Shorter working distances, limiting accessibility.
Shallower depth of field.
Requires more precise alignment and focus.
Higher NA lenses are often more sensitive to aberrations and more expensive.
In addition, NA interacts with image-side optics (explained next), impacting contrast and overall system fidelity.
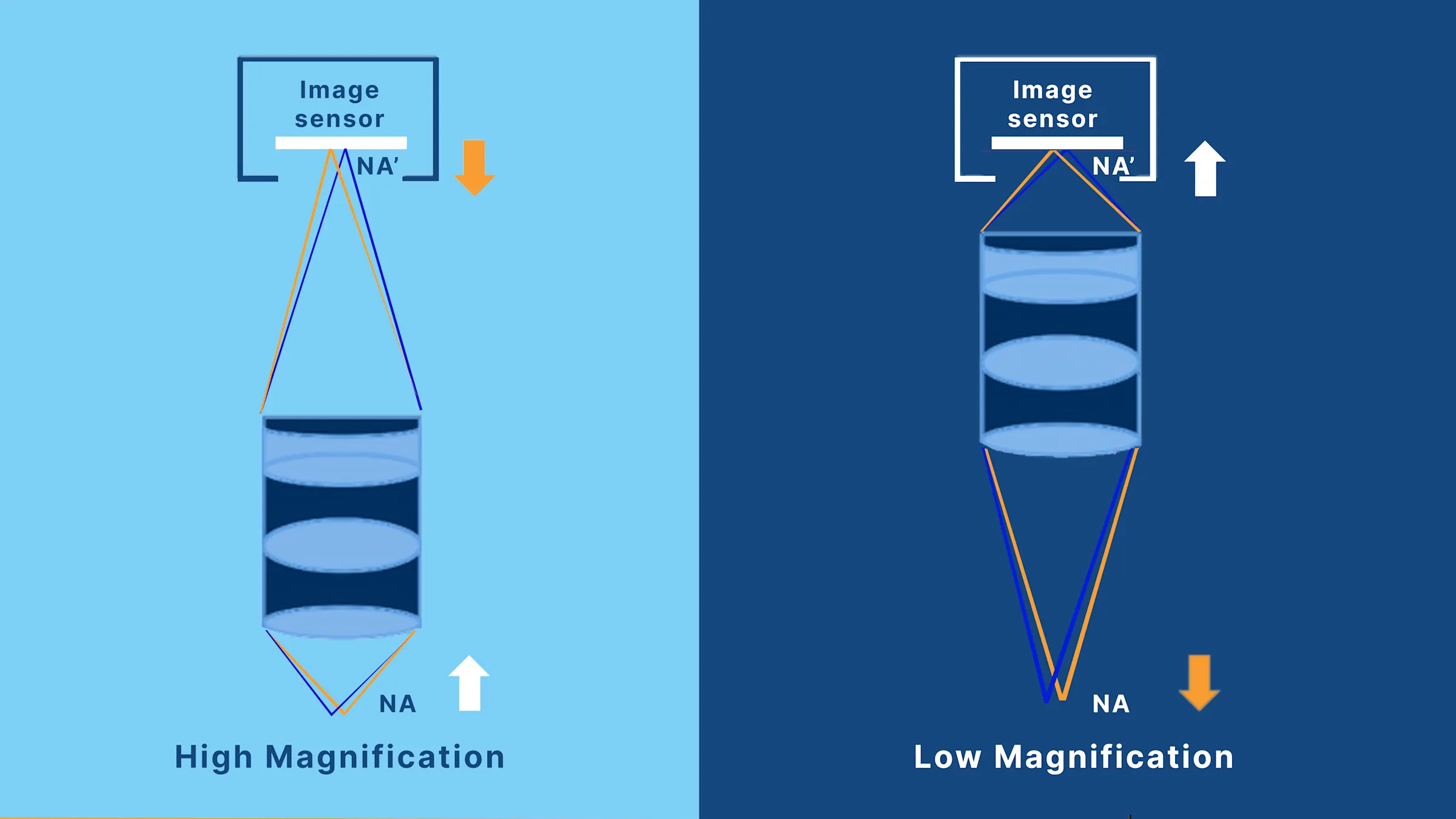
物方NA与像方NA(NA vs. NA′)
完整的成像系统同时包括物方与像方数值孔径,二者分别影响不同的图像质量:
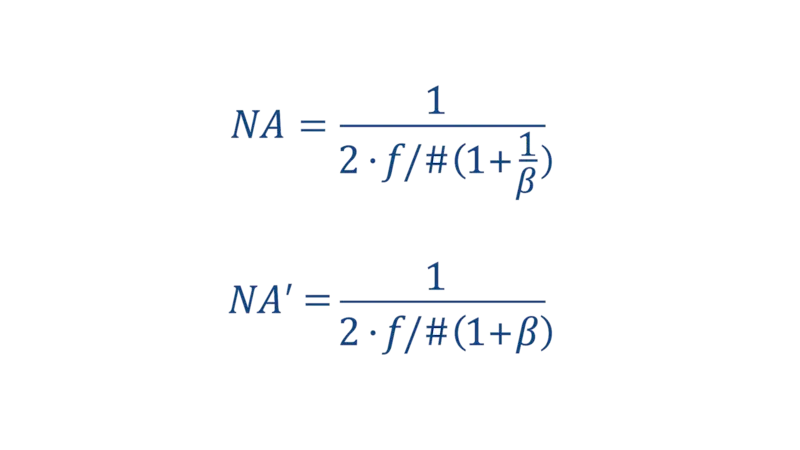
Definitions and equations
There are two kinds of NAs:
Object-side NA (NA): Between the sample and the objective lens
Image-side NA (NA′): Between the tube lens and the image sensor
These two NAs are related by the following equation:
NA = β X NA'
Where:
β: represents lateral magnification, defined as image size divided by object size.
This means that as magnification increases, the object-side NA increases while the image-side NA decreases. In practice, higher magnification is often used to achieve a larger NA for resolving smaller defects. However, this also reduces the image-side NA, which can lead to darker and blurrier images.

The trade-off between NA and NA′
This inverse relationship is critical for system design:
NA controls how small a feature can be resolved.
NA′ governs how clearly that feature is transferred to the sensor — i.e., contrast, particularly at high spatial frequencies.
NA′ is tied to the Modulation Transfer Function (MTF) — a measure of contrast across feature sizes. If NA′ is too low:
The MTF declines rapidly at high frequencies.
Fine details become poorly visible or even invisible, despite being technically resolved.
In a word, high NA without sufficient NA′ can produce images that are sharp but lack the contrast necessary for reliable inspection or measurement.
总结
在显微成像中,放大倍率、NA和分辨率必须协同作用,仅优化单一参数无法保证图像质量提升:
放大倍率控制特征在传感器上的显像大小,需与相机像元尺寸匹配以避免过采样或欠采样;
数值孔径(NA)决定镜头可分辨的最小特征尺寸。更高NA可提升细节与亮度,但会牺牲景深;
像方NA(NA′)影响细节传输至传感器的清晰度,决定对比度及高频信息的可见性。
核心要义:高放大倍率需高NA以保障分辨率,而二者都需足够的NA′以维持对比度。优秀的系统需协同考量分辨率、对比度和视场。
延伸阅读:若需深入了解包括阿贝衍射极限、瑞利判据、光学像差及奈奎斯特采样要求在内的系统级限制因素,请继续阅读《显微镜分辨率的真正限制因素》。
To the Article: What Really Limits Microscopy Resolution